√ダウンロード 平行 四辺 形 性質 539738

※例1のような性質は「平行四辺形の2組の向かい合う辺はそれぞれ等しい」と表現されることもある． 問題 四角形 abcd について左欄の性質を証明するとき，どのような仮定からどのような結論を導けばよいか．右の欄から選びなさい． （はじめに左欄の問題を1つ選び続けて右欄の答えを選び1 単元名 垂直・平行と四角形「四角形をつくろう」 2 単元とその指導について (1) 教材観 本単元では，以下の3点をねらいとしている。 ① 垂直，平行や台形，平行四辺形，ひし形の性質について調したがって、2つの対角線がおのおのの中点で交わる四角形は平行四辺形である。 5章(三角形と四角形) 2節(四角形) 3．平行四辺形の性質の定理の逆 年 組 番 名前 A O D B C A B C D E

高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形

平行 四辺 形 性質

平行 四辺 形 性質-こんにちは、ウチダショウマです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か平行四辺形の定義と性質 平行四辺形は，等しい辺や角がたくさんあります。 どこに目をつけて「平行四辺形」という名前を付けたかは名前を見れば分かりますね。 平行四辺形の定義は、2組の向かい合う辺がそれぞれ平行な四角形

2 1の授業と 総復習 得点力 数学 受験ブログ

数学25章図形の性質と証明「平行四辺形の性質」＜基本問題①＞ 組 番 名前 次の図を作図しなさい。 （1）平行四辺形ABCDを三角定規を使ってかきなさい。 （2）長方形ABCDを三角定規とコンパスを使って作図しなさい。平行四辺形とひし形の違いってなに？？ 平行四辺形の角度、辺の長さを求める問題を解説！ 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説！ 等積変形三角形の面積問題と作図のやり方は？証明問題も紹介！←今回の記事・平行四辺形の性質を利用して、図形の証明をすることができる。 ・証明の結果からわかった、新たな性質を理解することができる。 （2）本時の指導について 本時の授業では、関連づけを図る（別の場面に置き換える）課題を扱い、平行四辺形の性質

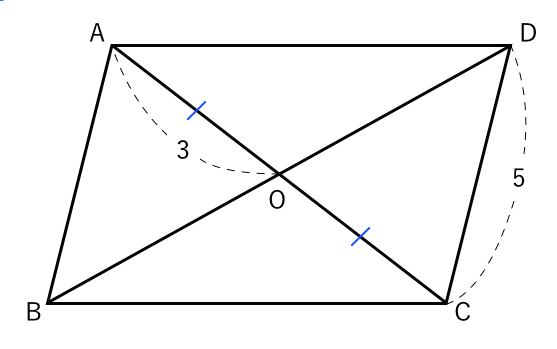
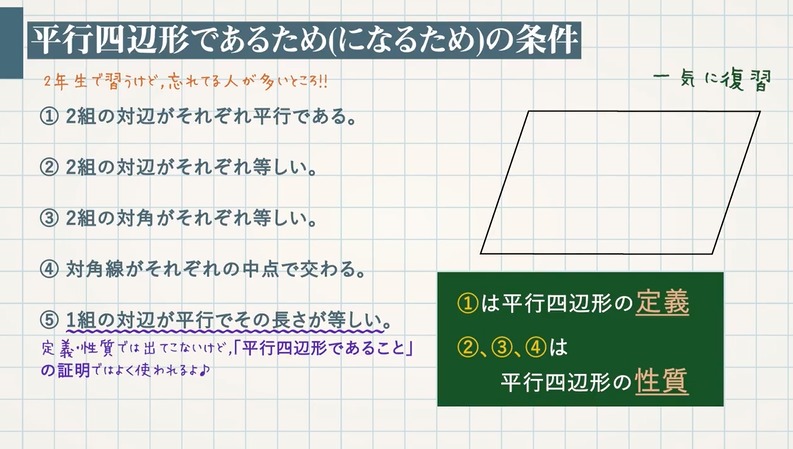
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。（定義） 2 2組の向かいあう辺が、それぞれ等しい。（証明） 3 2組の向かいあう角が、それぞれ等しい。（証明）対角線の意味、台形、平行四辺形、ひし形の概念と性質、作図などを、繰り返し練習することができます。 台形・平行四辺形・ひし形・対角線 (1) 答え 台形・平行四辺形・ひし形・対角線 (2) 答え 台形・平行四辺形・ひし形・対角線 (3) 答え 台形・平行四辺形・ひし形・対角線 (4) 答え平行四辺形の対角線はそれぞれの中点で交わるから ao＝co・・・② 対頂角は等しいから ∠aom＝∠con・・・③ ①～③より1組の辺とその両端の角がそれぞれ等しいから abd≡ con 合同な図形の対応する辺の長さは等しいからad=bc

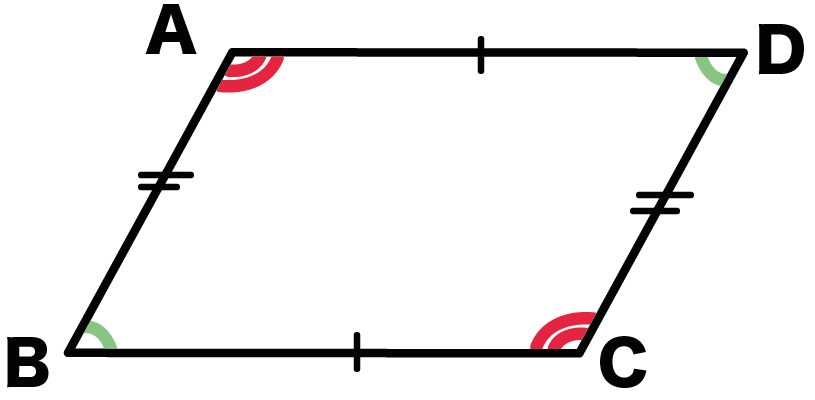
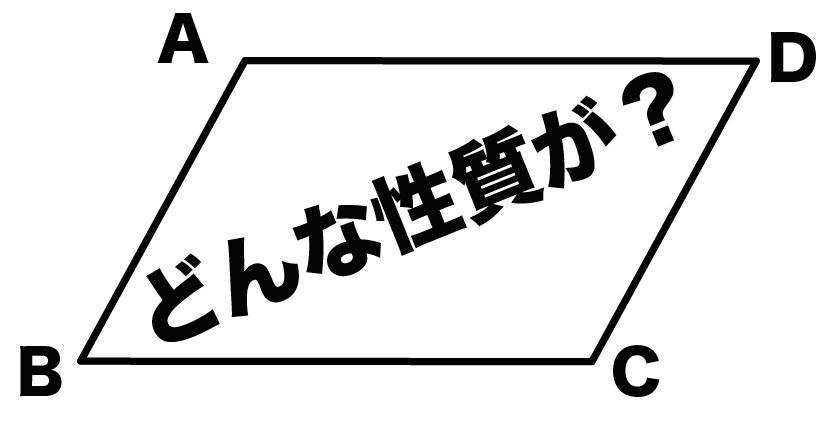
平行四辺形の性質 平行四辺形は、次のような性質を持つ。 対辺の長さが等しい（対辺は2組あるが、いずれもこの性質を満たす）。 対角の大きさが等しい（対角は2組あるが、いずれもこの性質を満た 予習や復習、反転授業にも使えます。 数学検定対策にもピッタリ。 大学入試改革も見すえた、意味からわかるミーニング数学。 数学苦手な学生ブリタニカ国際大百科事典 小項目事典 平行四辺形の用語解説 2組の対辺がともに平行である四角形。次のような性質をもつ。(1) 2組の対辺の長さはそれぞれ等しい。(2) 2組の対角の大きさはそれぞれ等しい。(3) 2本の対角線はそれぞれの中点で交わる。1組の対辺が平行な四角形は台形なので

2 1の授業と 総復習 得点力 数学 受験ブログ

平行四辺形の定義と性質 証明問題の解き方 数学fun

 31 平行四辺形の性質その1：対辺の長さが等しい 32 平行四辺形の性質その2：対角の大きさが等しい 33 平行四辺形の性質その3：対角線が他の対角線の中点を通る 4 平行四辺形の面積平行四辺形の性質を利用した証明 ao=co (平行四辺形の対角線はそれぞれの中点で交わる) ∠aoe=∠cof (対頂角) ∠eao=∠fco (ab//cd 錯角) 1組の辺とその両端の角がそれぞれ等しいので aeo≡ cfo 合同な三角形の対応する辺は等しいので ae=cf平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ

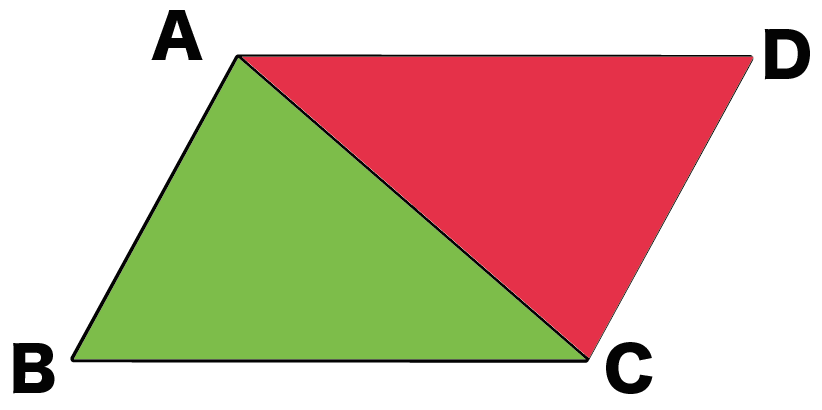
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく

小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

平行四辺形の定義 二組の対辺がそれぞれ平行な四角形を 平行四辺形 という。 性質① 2組の対辺はそれぞれ等しい。平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図） 1 平行四辺形の向かい合う辺は等しい。（証明） 2 平行四辺形の向かい合う角 平行四辺形という仮定(2組の対辺がそれぞれ平行)だけでは、どこも辺が等しいことがいえないからだ。 そこで1番を先に証明することが必要になる。 まとめると平行四辺形の性質は 3が本質。 1は3を証明するための補題。 2は1の証明から獲れるオマケ。

やり方を教えてください Clear

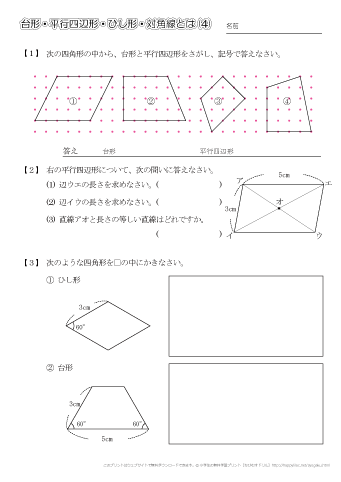
小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

(2) 平行四辺形の性質や平行四辺形であるための条件を見いだし，論理的に確かめることができる。 (3) 平行線を使った等積変形について理解することができる。 (4) 証明した図形の性質を，いろいろな場面で活用することができる。 6 単元の評価規準 数学への平行四辺形の定義 (AB//CD, AD//CB)から、「対角線はそれぞれの中点で交わる」を証明する。 A B C D O平行四辺形の性質 名前 下の（ ）にあてはまる適当な言葉を書きなさい。 ①平行四辺形の定義 2組の（ ）がそれぞれ（ ）な四角形。 ②平行四辺形の性質 ア2組の（ ）はそれぞれ等しい。

高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形

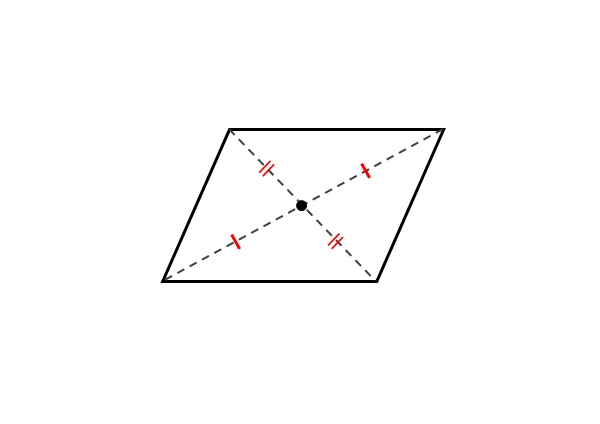
図形と方程式 平行四辺形の頂点の座標について 日々是鍛錬 ひびこれたんれん

平行四辺形の特徴は、 ① 「2組の対辺（向かい合う辺）が、それぞれ平行」 に加えて、残り3つ。 キーワードは、 「辺」 、 「角」 、 「対角線」 だよ。 まずは、 「辺」 から。 ② 「2組の対辺がそれぞれ等しい」 向かい合う辺の長さ が、それぞれ等しいんだね。 次に、 「角」 。 ③ 「2組の対角がそれぞれ等しい」平行四辺形の向かい合う角は等しいので， a ＝110° 同様にして，四角形GDFI も平行四辺形で， b ＝∠DGI＝180°－ a ＝180°－110°＝70° また，平行四辺形の向かい合う辺は等しいので， x ＝CF 7 －4 3cm， y AG 10 6 4cm 問題(後期期末)下の図は特別な平行四辺形をまとめたものです。それぞれの にあてはまる語をいれて、 文章を完成させなさい。 2 下の図は、四辺形をまとめたものです。①から⑤にあてはまる四角形の名称を答えなさい。 ① ② ③ ④ ⑤

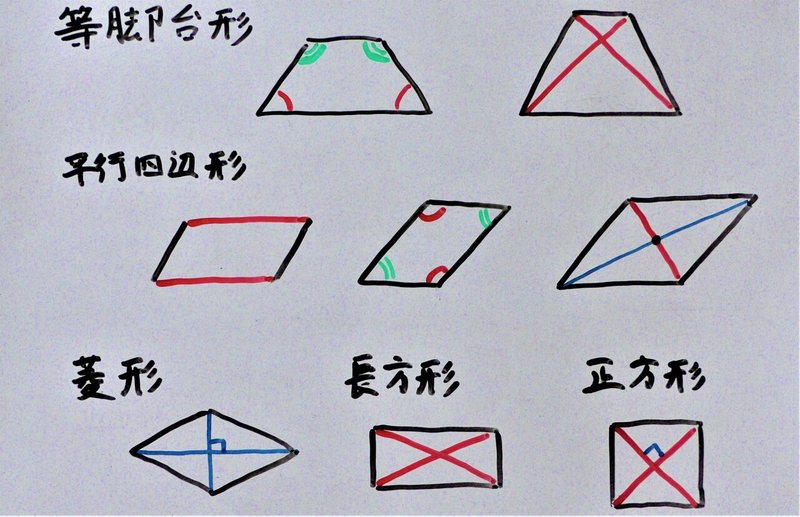
9 3 平面の幾何 準備 四角形 理一の数学事始め Note

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

平行四辺形の定義と性質 証明問題の解き方 数学fun For more information and source, see on this link https//sugakufun/parallelogramnature/

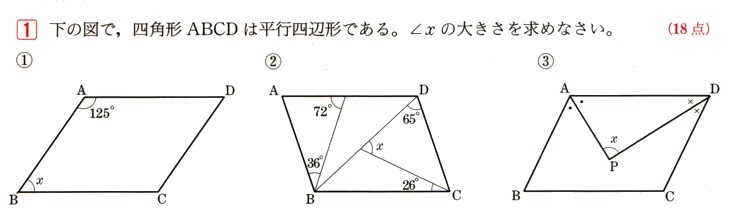
中学２年数学 平面図形 平行四辺形の性質 確認問題１ あんのん塾

雑学のソムリエ テボールの定理

2 64 第４章 平行四辺形 平行四辺形の性質を使った証明 Kakera Link 公式ブログ

Www Pref Osaka Lg Jp Attach Cyuu2goudou3kaku4kaku Pdf

スタディピア 図形

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

平行四辺形の例題 ぼーの秘密部屋

1

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

B 2 Descubre Como Resolverlo En Qanda

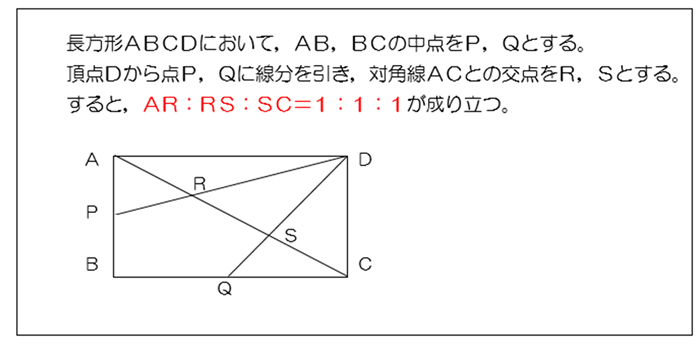
授業実践記録 数学 新しい 定理 とその活用 啓林館

中2数学第5章6平行四辺形になるための条件 応用 Youtube

Www Nier Go Jp Jugyourei H25 Pdf Idea Jm 3 Pdf

平行四辺形になるための条件 Youtube

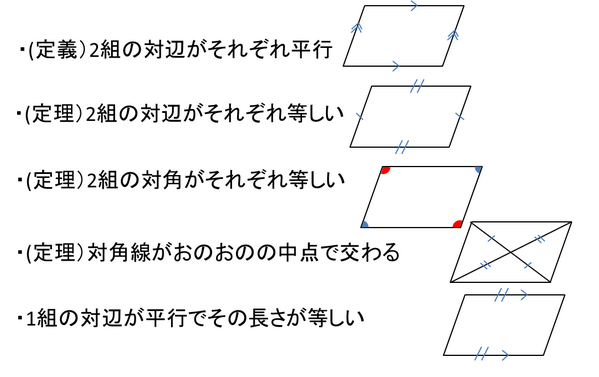
140字で高校受験 En Twitter 数学 平行四辺形の定義 性質 なるための条件 言葉だけでなく図で覚える T Co Amwmvf58n7

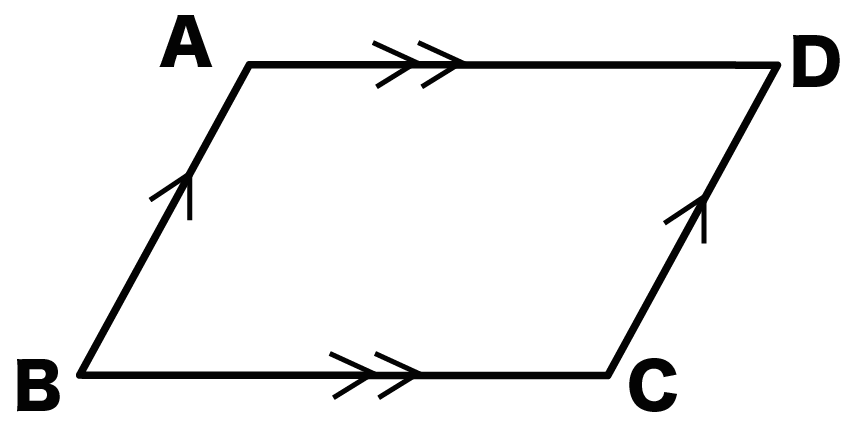
3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく

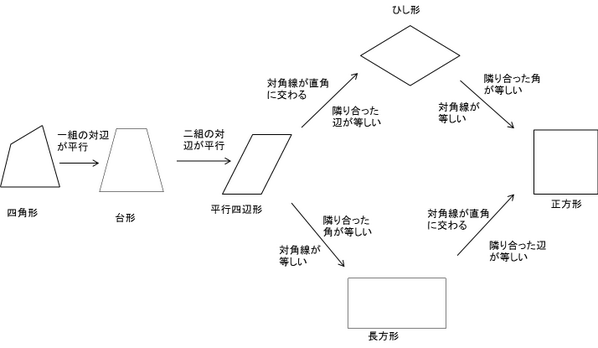
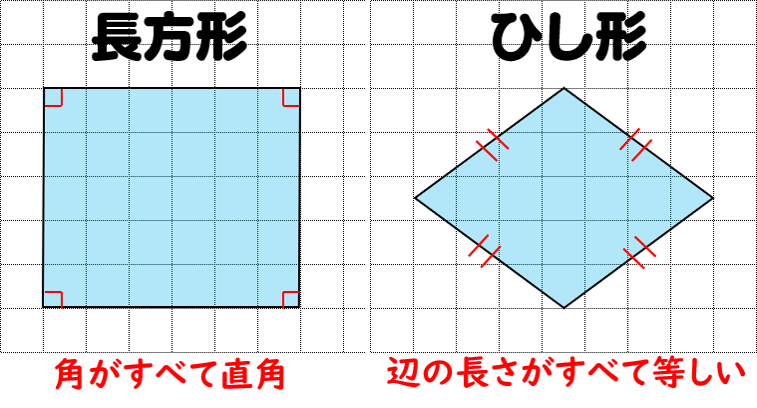
140字で高校受験 数学 四角形の性質まとめ 四角形 台形 平行四辺形 長方形 ひし形 正方形 高校受験 数学 T Co Tumufb1q86

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

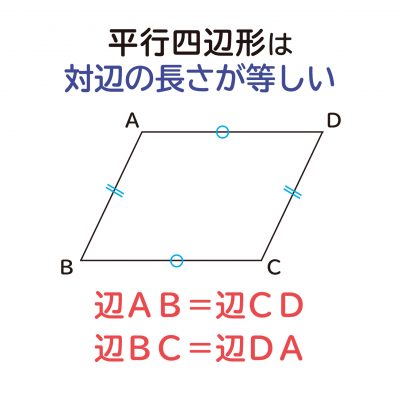
平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

File 平行四辺形の性質 2 Png Wikimedia Commons

平行四辺形 中学数学で遊ぶ 身勝手な主張

中2数学第5章5平行四辺形の性質を利用した証明 応用 Youtube

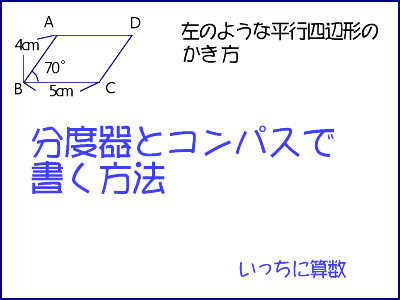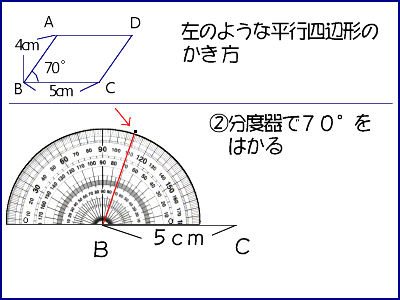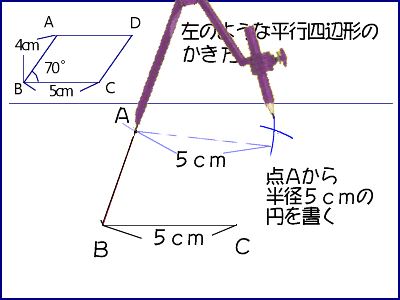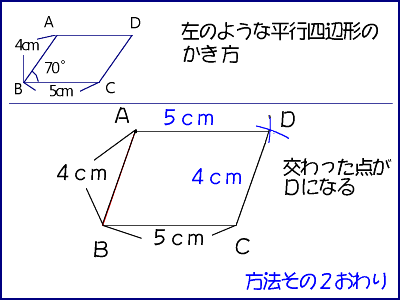
４年算数 垂直 平行と四角形 ２ 教え方

高校入試 英語 数学 学習 三角形と四角形 平行四辺形

中2数学 平行四辺形の性質の利用 例題編 映像授業のtry It トライイット

外積の長さ 平行四辺形の面積 証明 理数アラカルト

四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究

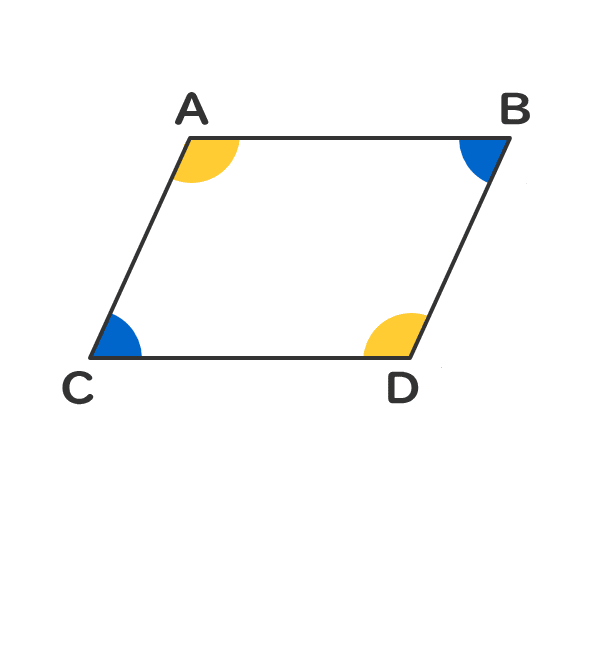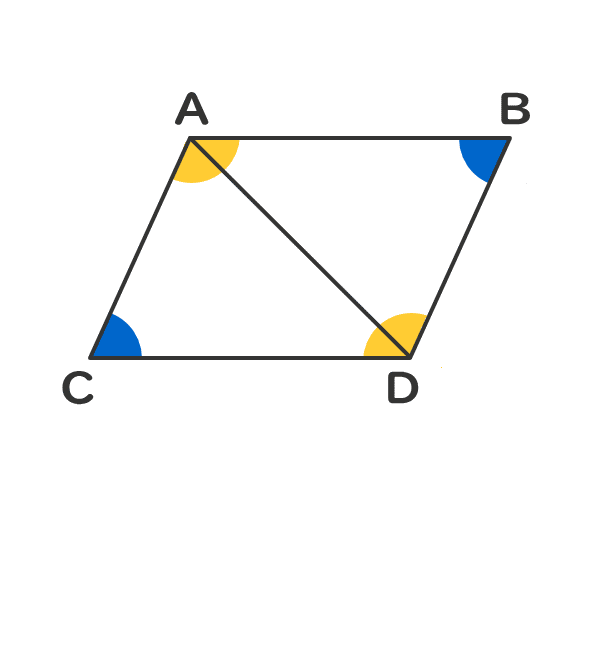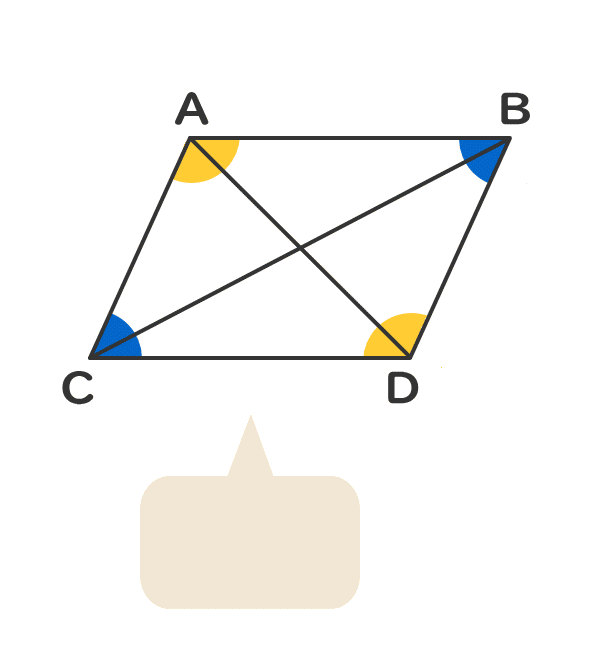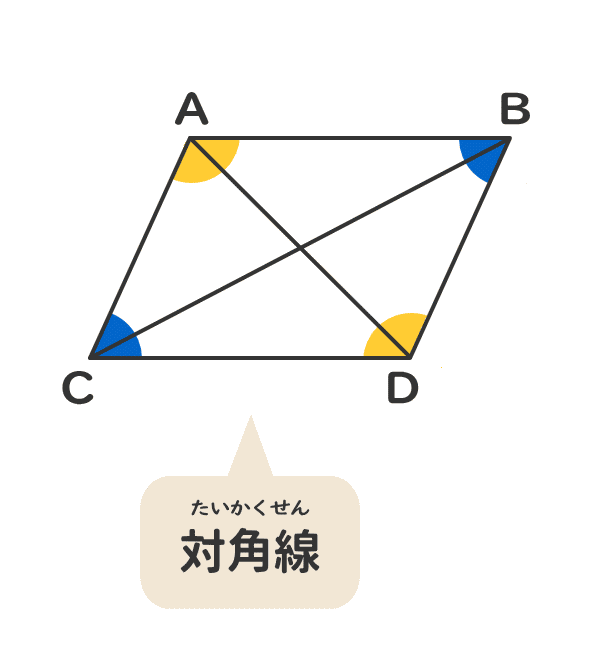
平行四辺形の仲間を知ろう 電験3種web

Www Edu City Yokohama Lg Jp Sch Kenkyu Es Sansu Pdf R2 Kou510 Pdf

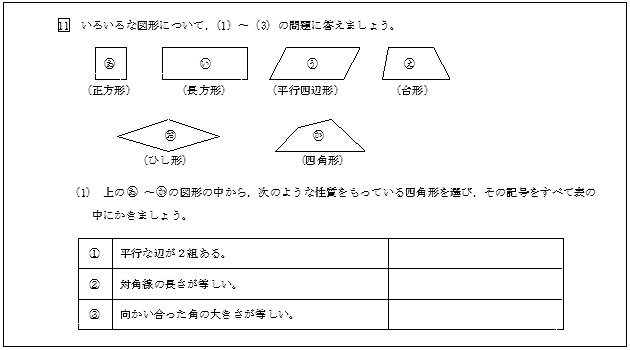
第1章 7 図形 領域における教科書記述の研究 文部科学省

平行四辺形の性質 と ひし形の性質 を比べる とちぎｅライブラリ

1

1

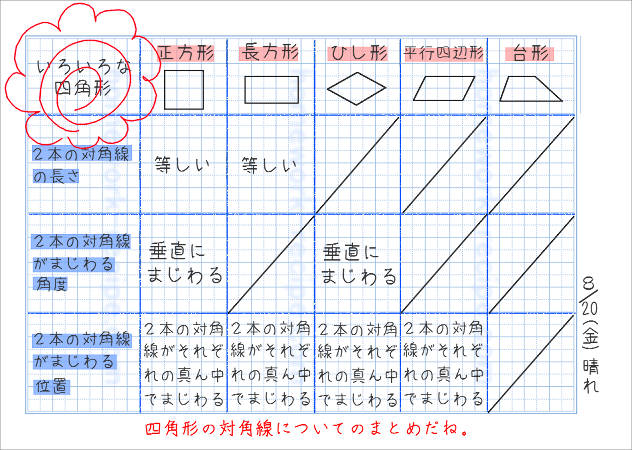
いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ

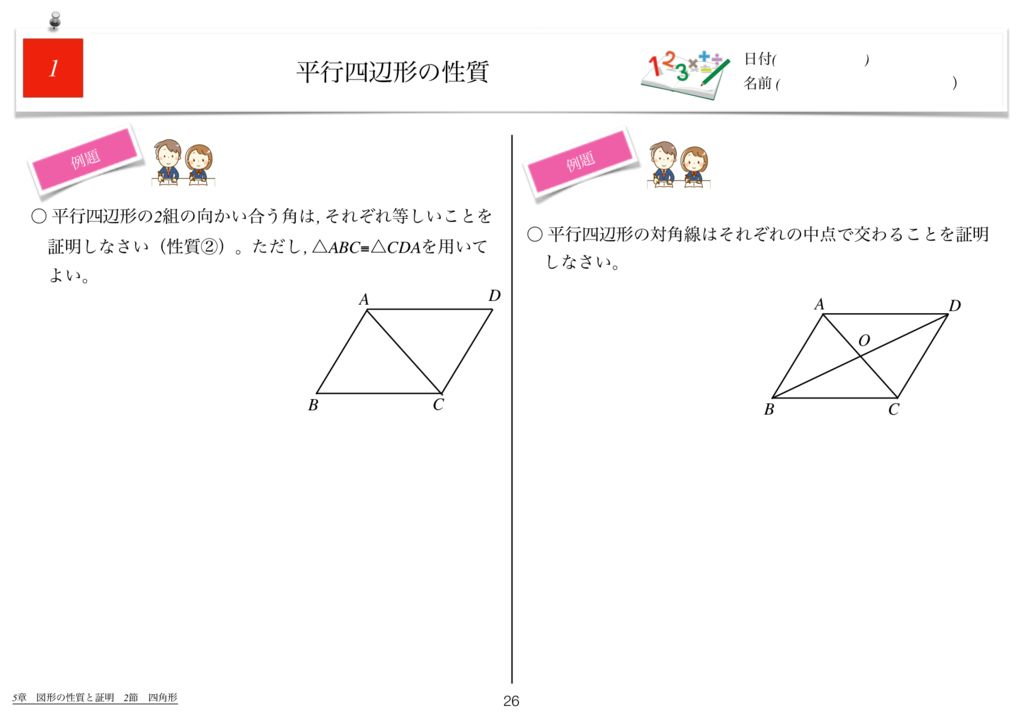
世界一わかりやすい数学問題集中２ ５章 図形の性質と証明

75 平行 四辺 形 証明 解き方 最高のぬりえ

1 4 Lihat Cara Penyelesaian Di Qanda

平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

5 Ay C F See How To Solve It At Qanda

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット

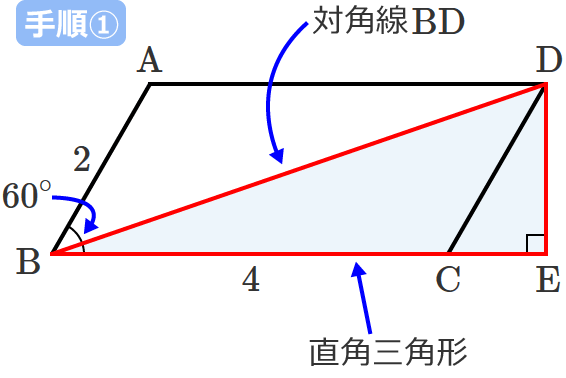
ベスト平行四辺形 対角線 長さ ベクトル 最高のぬりえ

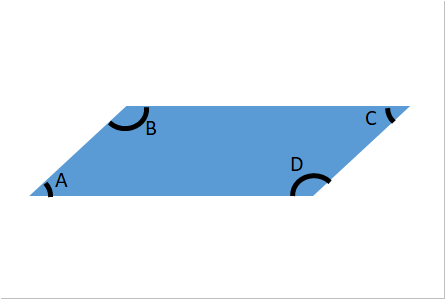
小4 B 四角形 平行四辺形の性質 向かい合う辺 向かい合う角が同じ

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

世界一わかりやすい数学問題集中２ ５章 図形の性質と証明

トップ100平行四辺形 対角線 長さ 違う 最高のぬりえ

中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく

中学2年 平行四辺形の性質 つみき書店

平行四辺形について知ろう 苦手な数学を簡単に

平行四辺形 中学数学で遊ぶ 身勝手な主張

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

平行四辺形の証明問題 無料で使える中学学習プリント

平行四辺形の性質 イ弋マ本ゼミナール

中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく

動画で学習 3 台形と平行四辺形 算数

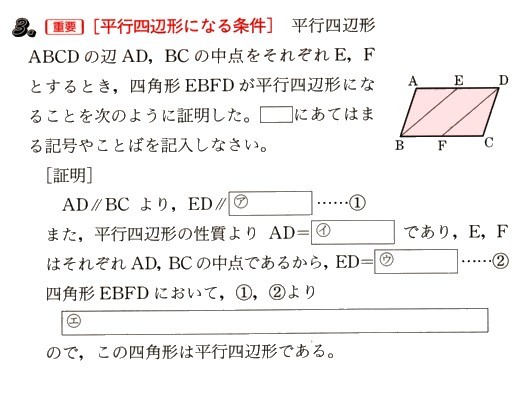
中学２年数学 平行四辺形の性質 練習問題３ あんのん塾

45 5times3 See How To Solve It At Qanda

中点連結定理を使った平行四辺形であることの証明 教遊者

解説をお願いします Clear

Dfrac32qc 2 Oqc10cm2 2 Descubre Como Resolverlo En Qanda

世界一わかりやすい数学問題集中２ ５章 図形の性質と証明

平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

3 3 Abcd Ab9cm 5cm D See How To Solve It At Qanda

平行四辺形の性質 Clear

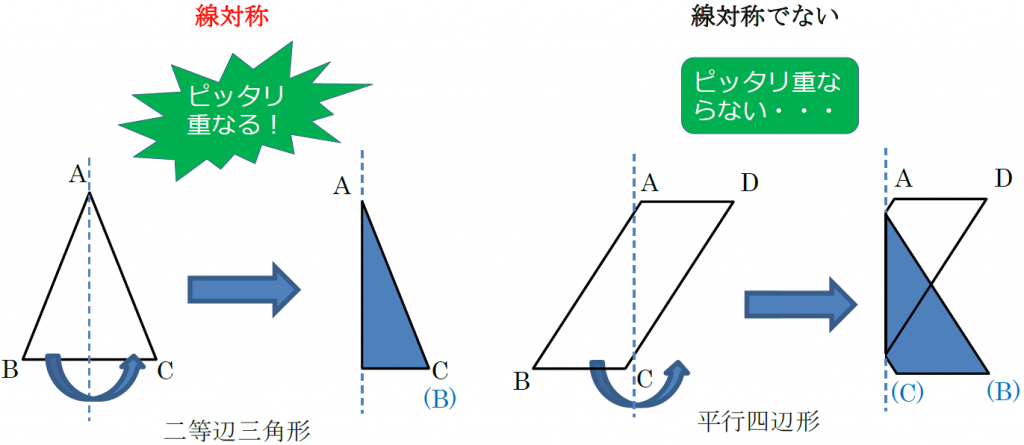
中１数学 点対称な図形とは まなビタミン

ボード 勉強 のピン

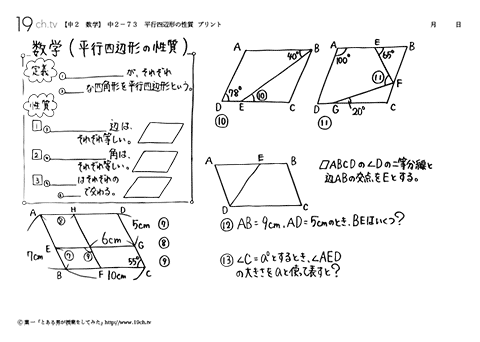
中学2年の数学 動画 平行四辺形の性質の問題 19ch

3つの手筋 図形 後編 公務員試験知能 教員採用試験数学解説

1

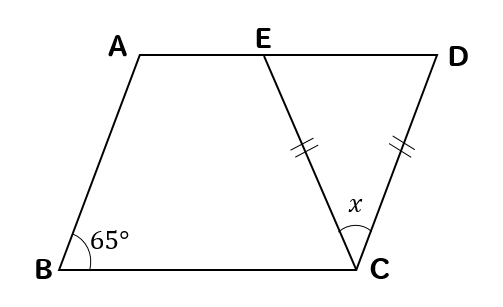
平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

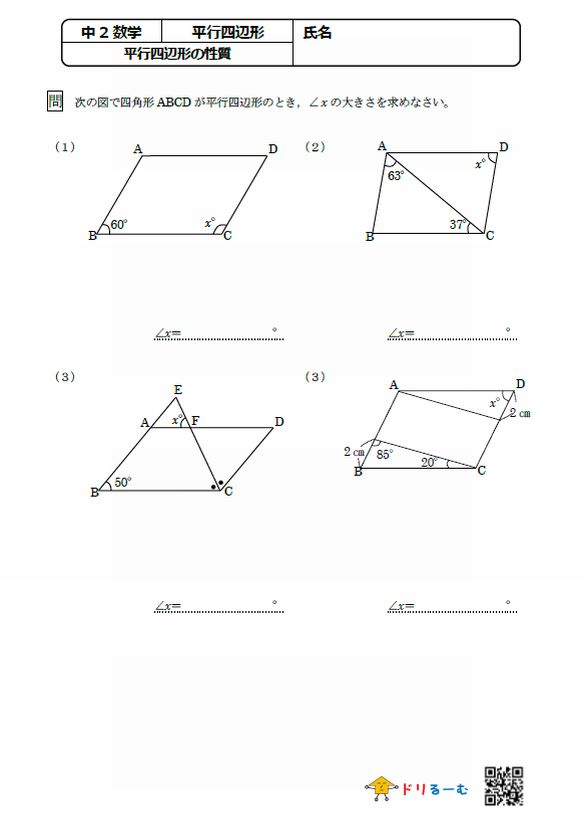
平行四辺形の性質 ドリるーむ

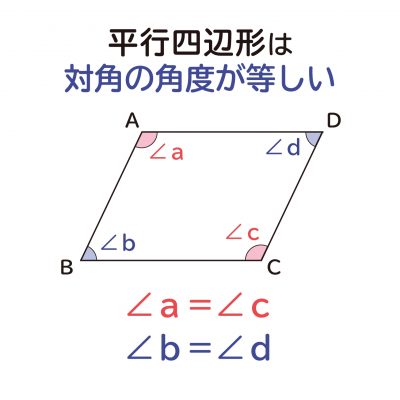
平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

平行四辺形の座標 数学ii By Okボーイ マナペディア

平行四辺形の性質を全部教えてください Clear

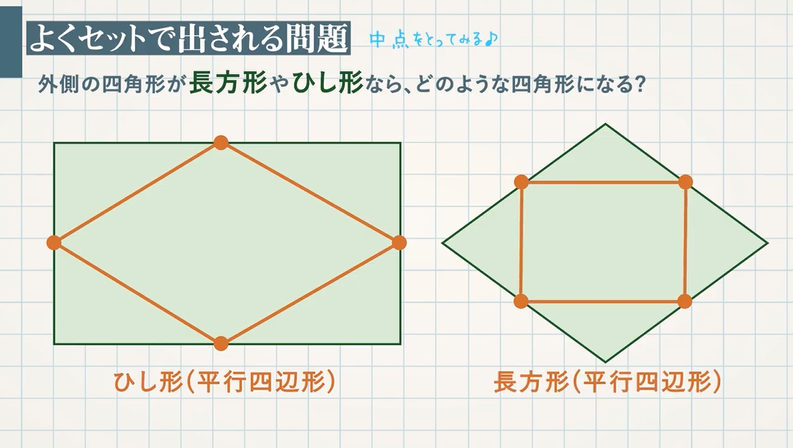
中点連結定理を使った平行四辺形であることの証明 教遊者

四辺形 Japaneseclass Jp

世界一わかりやすい数学問題集中２ ５章 図形の性質と証明

簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 図形の合同 図形の性質

中学数学 特別な平行四辺形について Clear

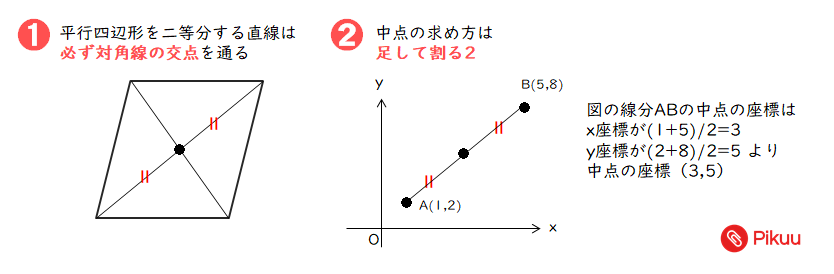
中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu

無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch

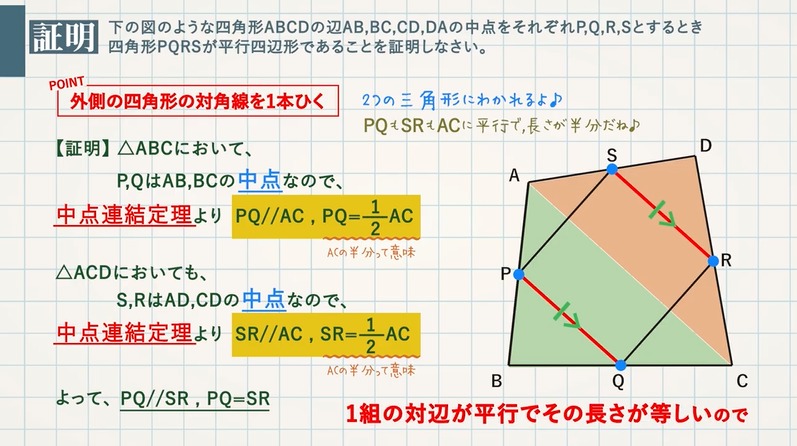
中点連結定理を使った平行四辺形であることの証明 教遊者

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

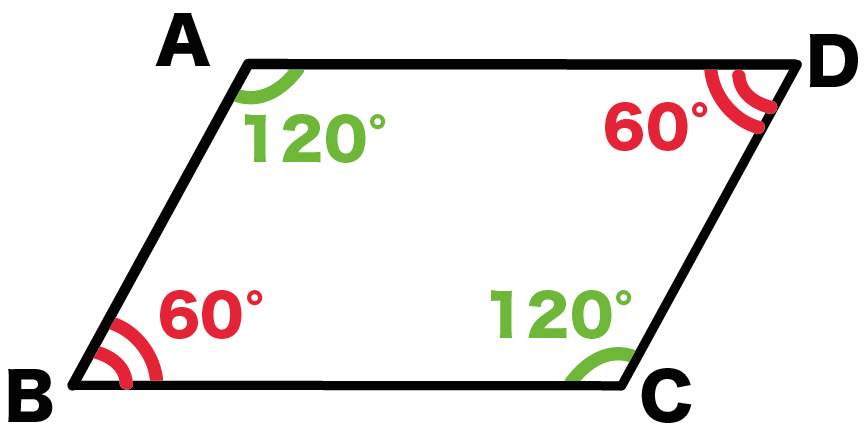
中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく

ひし形の定義 性質 条件 Youtube

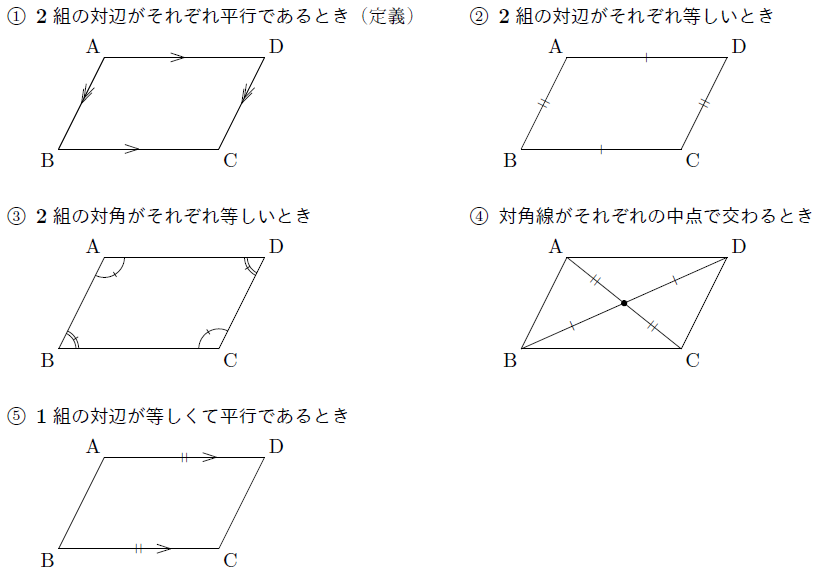
平行四辺形になるための条件 まなびの学園

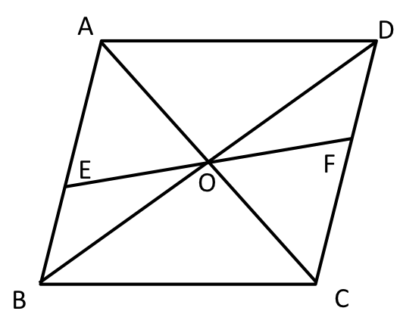
フロー 2 5 5 2 平行四辺形の性質を利用した証明

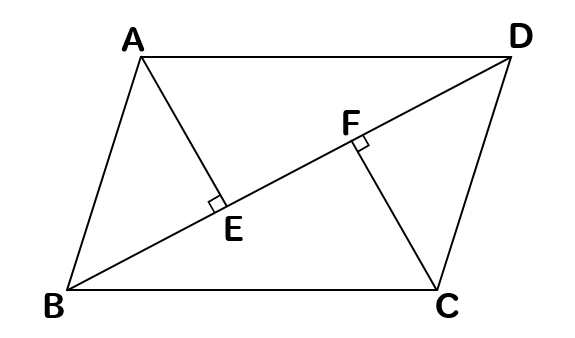
中学数学 平行四辺形の証明問題を徹底解説 数スタ

中学２年数学 平行四辺形の性質 練習問題５ あんのん塾

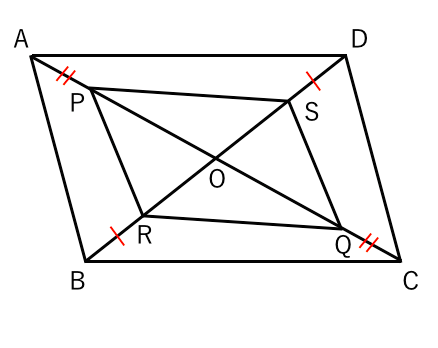
平行四辺形であることを証明する 苦手な数学を簡単に

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

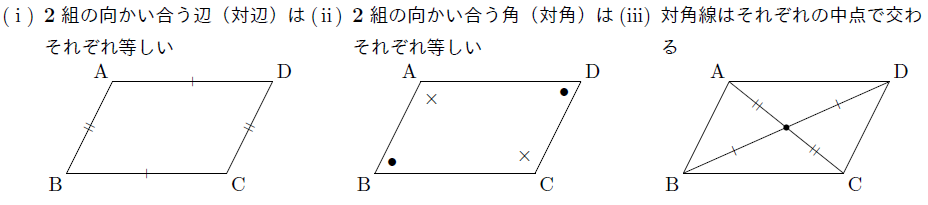
平行四辺形の性質 まなびの学園